给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目

请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n

示例 1：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素

示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]
解释：需要合并 [1] 和 [] 
合并结果是 [1]

示例 3：

输入：nums1 = [0], m = 0, nums2 = [1], n = 1
输出：[1]
解释：需要合并的数组是 [] 和 [1] 
合并结果是 [1] 
注意，因为 m = 0 ，所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中

官方解法

方法一：合并后直接排序

最直观的方法是先将数组 nums2 放进数组 nums1 的尾部，然后直接对整个数组进行排序

public void merge(int[] nums1, int m, int[] nums2, int n) {
    for (int i = 0; i < n; ++i) {
        nums1[m + i] = nums2[i];
    }
    Arrays.sort(nums1);
}

复杂度分析

• 时间复杂度：O((m+n)log(m+n))。排序序列长度为 m+n，套用快速排序的时间复杂度即可，平均情况为 O((m+n)log(m+n))

• 空间复杂度：O(log(m+n))。排序序列长度为 m+n，套用快速排序的空间复杂度即可，平均情况为 O(log(m+n))

方法二：双指针

算法

方法一没有利用数组 nums1 与 nums2 已经被排序的性质。为了利用这一性质，我们可以使用双指针方法。这一方法将两个数组看作队列，每次从两个数组头部取出比较小的数字放到结果中。如下面的动画所示：

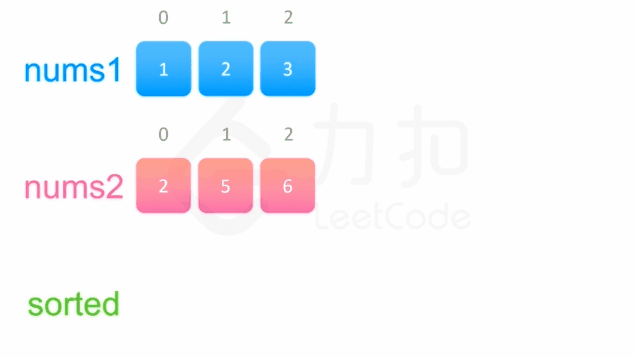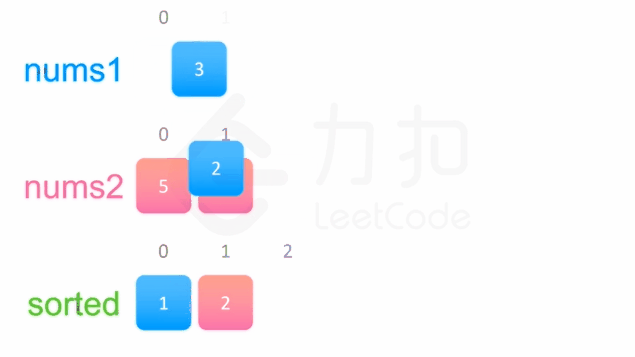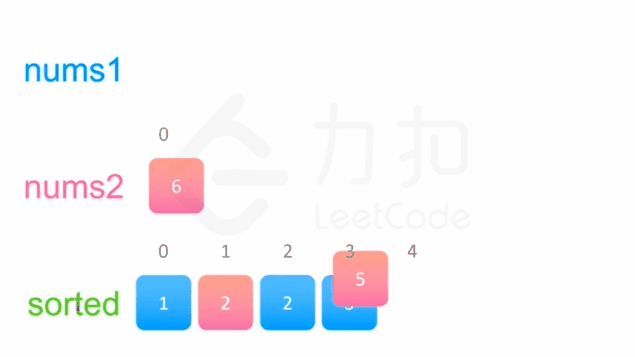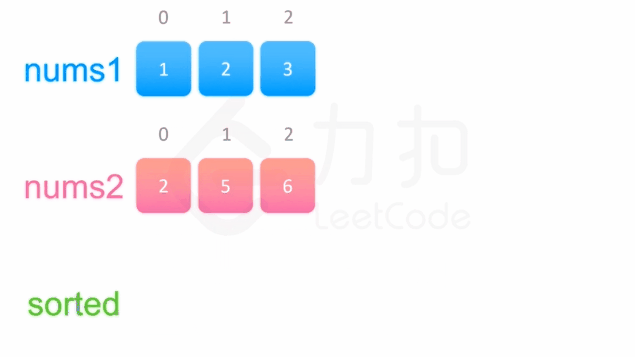
public static void merge(int[] nums1, int m, int[] nums2, int n) {
    int p1 = 0, p2 = 0;
    int[] sorted = new int[m + n];
    int cur;
    while (p1 < m || p2 < n) {
        if (p1 == m) {
            cur = nums2[p2++];
        } else if (p2 == n) {
            cur = nums1[p1++];
        } else if (nums1[p1] < nums2[p2]) {
            cur = nums1[p1++];
        } else {
            cur = nums2[p2++];
        }
        sorted[p1 + p2 - 1] = cur;
    }
    for (int i = 0; i < m + n; i++) {
        nums1[i] = sorted[i];
    }
}

复杂度分析

• 时间复杂度：O(m+n)。指针移动单调递增，最多移动 m+n 次，因此时间复杂度为 O(m+n)

• 空间复杂度：O(m+n)。需要建立长度为 m+n 的中间数组 sortedsorted

解法三：逆向双指针

方法二中，之所以要使用临时变量，是因为如果直接合并到数组 nums1 中，nums1 中的元素可能会在取出之前被覆盖。那么如何直接避免覆盖 nums1 中的元素呢？观察可知，nums1 的后半部分是空的，可以直接覆盖而不会影响结果。因此可以指针设置为从后向前遍历，每次取两者之中的较大者放进 nums1 的最后面。严格来说，在此遍历过程中的任意一个时刻，nums1 数组中有 m - p1 -1 个元素被放入 nums1 的后半部，nums2 数组中有 n - p2 -1 个元素被放入 nums1 的后半部，而在指针 p1 的后面，nums1 数组有 m + n - p1 -1 个位置。由于 m + n − p1 −1 ≥ m − p1 −1 + n − p2 ​− 1 等价于 p2 ≥ −1 永远成立，因此 p1 ​后面的位置永远足够容纳被插入的元素，不会产生 p1 ​的元素被覆盖的情况

public static void merge(int[] nums1, int m, int[] nums2, int n) {
    int p1 = m - 1, p2 = n - 1;
    int tail = m + n - 1;
    int cur;
    while (p1 >= 0 || p2 >= 0) {
        if (p1 == -1) {
            cur = nums2[p2--];
        } else if (p2 == -1) {
            cur = nums1[p1--];
        } else if (nums1[p1] > nums2[p2]) {
            cur = nums1[p1--];
        } else {
            cur = nums2[p2--];
        }
        nums1[tail--] = cur;
    }
}

复杂度分析

• 时间复杂度：O(m+n)。指针移动单调递减，最多移动 m+n 次，因此时间复杂度为 O(m+n)

• 空间复杂度：O(1)。直接对数组 nums1 原地修改，不需要额外空间

自解

直接数组合并排序就完事了

public static void merge(int[] nums1, int m, int[] nums2, int n) {
    for (int i = m, j = 0; i < nums1.length; i++, j++) {
        nums1[i] = nums2[j];
    }
    Arrays.sort(nums1);
}