插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

算法描述

一般来说，插入排序都采用 in-place 在数组上实现。具体算法描述如下：

• 从第一个元素开始，该元素可以认为已经被排序

• 取出下一个元素，在已经排序的元素序列中从后向前扫描

• 如果该元素（已排序）大于新元素，将该元素移到下一位置

• 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置

• 将新元素插入到该位置后

• 重复步骤2~5

动图演示

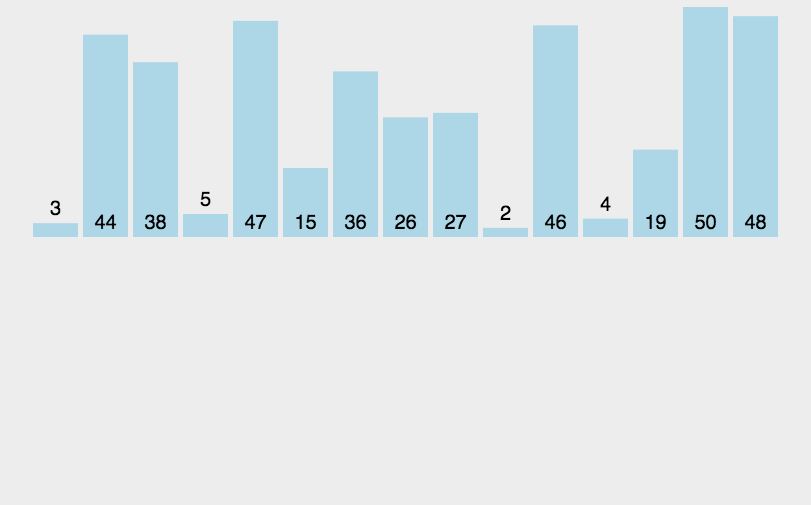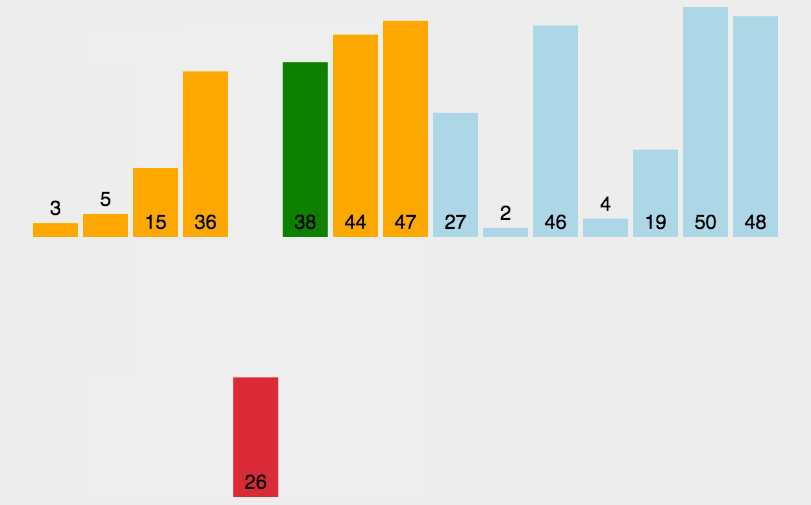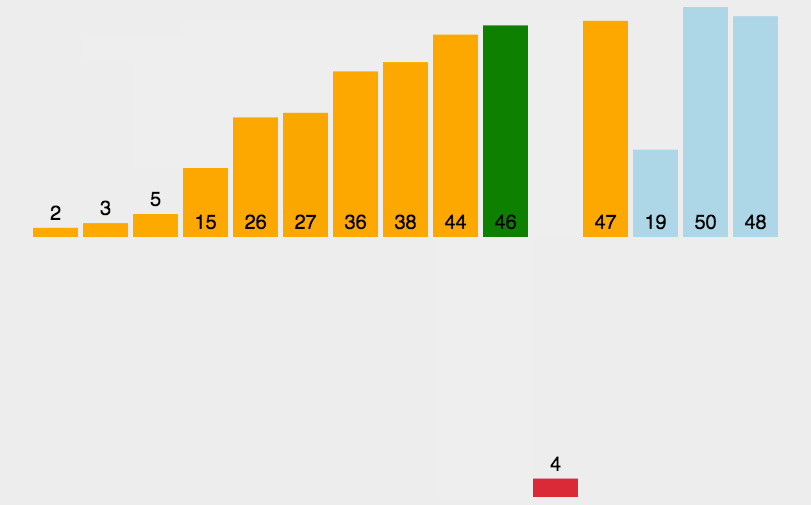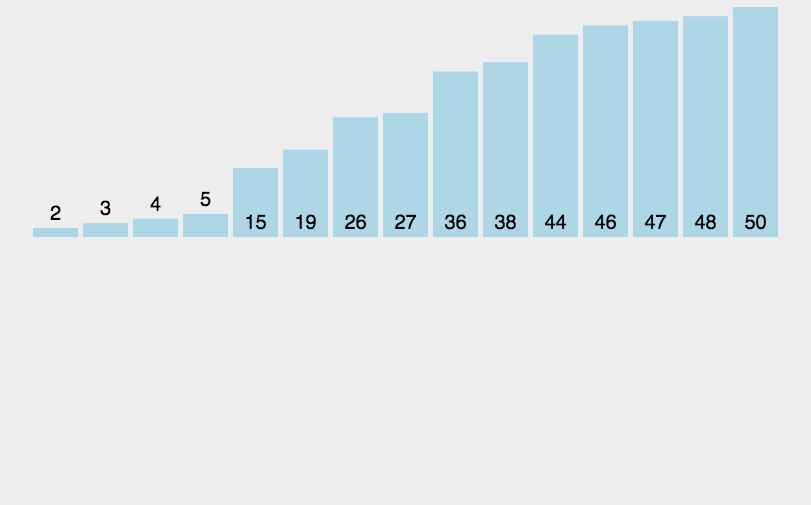
代码实现

public static void main(String[] args) {
    int[] array = {3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48};

    insertionSort(array);

    System.out.println(Arrays.toString(array));
}

public static void insertionSort(int[] array) {
    if (array == null || array.length <= 1) {
        return;
    }

    int length = array.length;
    // 要插入的数
    int insertNum;

    for (int i = 1; i < length; i++) {
        insertNum = array[i];
        // 已经排序好的元素个数
        int j = i - 1;
        while (j >= 0 && array[j] > insertNum) {
            // 从后到前循环，大于 insertNum 的数向后移动一位
            array[j + 1] = array[j];
            j--;
        }
        // 将需要插入的数放在要插入的位置
        array[j + 1] = insertNum;
    }
}

算法分析

最佳情况：T(n) = O(n) 最坏情况：T(n) = O(n2) 平均情况：T(n) = O(n2)